讲座题目：Strong attractors for the structurally damped Kirchhoff wave

models with subcritical-critical nonlinearities

主办单位：长江大学信息与数学学院

报告专家：杨志坚（郑州大学教授、博士生导师）

报告时间：2023年5月19日9：30-10：30

会议地点：8-406

专家简介：杨志坚 郑州大学理学博士，日本九州大学数理学博士，郑州大学2级教授，博士生导师，河南省跨世纪学术、技术带头人, 河南省高层次人才，美国 《Mathematical Reviews》评论员，《Journal of Partial Differential Equations》期刊编委。主要研究非线性发展方程的整体适定性及无穷维耗散动力系统的长时间动力学行为。主持完成4项国家自然科学基金面上项目；已在《J. Differential Equations》、《Nonlinearity》、《Commun. Contemp. Math.》、《J. Dyn. Differ. Equ.》、《Discrete Contin. Dyn. Syst.》、《J. Evol. Equ.》等国内外SCI期刊上发表研究论文90篇。获得河南省科技进步二等奖1项。

摘要：In this talk, we are concerned with the well-posedness and the regularity of the solutions, the existence and the continuity of the strong attractors for the structurally damped Kirchhoff wave models with subcritical-critical nonlinearities:

,

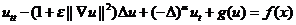where 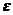∈[0, 1] is a perturbed extensibility parameter, 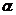∈[1/2, 1) is a dissipative index. We show that when the nonlinearity g(u) is of either critical growth as 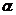∈(1/2, 1) or subcritical growth as 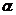= 1/2, while h(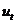) is of critical growth depending the 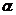, the model is well-posed and its weak solution is exactly the strong one; the related solution semigroup 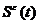has a strong (X, Y )-global attractor and a strong(X, Y )-exponential attractor, which are also the standard global and exponential attractor of optimal regularity of 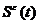in X, respectively, where X is the energy space and Y is the strong solution space; these global attractors are upper semicontinuous and these exponential attractors are Holder continuous with respect to perturbed parameter 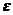in the sense of Y -topology, respectively. This work is joint with Fang Da and Yue Sun.